Dossier écrit présenté dans l’épisode #186 de Podcast Science
Les algorithmes de tri
En passant à la machine à café, vous avez sans doute déjà croisé des développeurs. Vous avez sans doute constaté qu’ils ont l’air passionnés par leur métier, ce qui rend leurs discussions animées. Et vous les avez sans doute entendu prononcer des mots comme « Bubble », « Quicksort », « logarithme » ou encore « complexité », qui semblent provenir d’une autre langue. Dans ce dossier, nous allons tenter de démystifier ce charabia.
« Bubble », « Quicksort », « Insertion » ou encore « Fusion » (pour ne citer qu’eux) sont les noms donnés à des algorithmes de tri célèbres. Wikipedia indique[1] qu’un algorithme est « une suite finie et non ambigüe d’opérations ou d’instructions permettant de résoudre un problème ». Et pour paraphraser ce qu’expliquait Nicotupe dans l’épisode 82[2], un algorithme de tri est en quelques sortes la « recette de cuisine » permettant à un logiciel de ranger les éléments d’une liste.
On veut trier une liste lorsqu’on pense que ses éléments sont dans le désordre, ou plus précisément dans un ordre qui ne nous convient pas. L’objectif du tri, en tant qu’algorithme, est de mettre les éléments dans le bon ordre. Trier une liste suppose donc qu’on est capable d’établir une relation d’ordre entre ses éléments (ce qui n’est pas toujours simple et/ou possible). Par exemple, on peut dire si Nicolas est (objectivement) plus petit que David. Quand je parle de « plus petit », je fais instinctivement référence à la taille des personnes, mais on aurait tout aussi bien pu comparer leurs poids, leurs quantités de cheveux, leurs notes au baccalauréat, etc. Mais pour simplifier, disons juste qu’on se base sur le critère de la taille.
Si ce sujet revient souvent chez les développeurs, c’est parce que le besoin de trier des données est omniprésent dans les programmes informatiques. Par habitude ou par inattention, on ne réalise pas qu’on manipule sans arrêt des données triées. Par exemple, disons qu’on s’intéresse à votre compte bancaire. Sur votre relevé, les opérations sont triées par date. Quand vous souscrivez à l’option Web, vous avez également la possibilité de trier selon les entêtes des colonnes (montant, date, numéro d’opération, bénéficiaire, type, etc.), mais vous ne vous êtes probablement jamais dit qu’il y avait un algorithme efficace caché derrière cette fonctionnalité.
Avant d’aller plus loin, je dois préciser qu’il existe des bons et des mauvais algorithmes de tri. Quand on tri une petite liste et qu’on le fait rarement, même le plus mauvais des algorithmes fera l’affaire. Par contre, quand on manipule des listes conséquences et/ou qu’on les trie souvent, il faut choisir avec attention l’algorithme qui sera le plus adapté au contexte.
Les premières manières qui nous viennent à l’esprit
Tri par sélection
Sans le savoir, où sans s’en rendre compte, on est confronté très jeune à des algorithmes de tri. Je dirais que cela se produit au plus tard en petite section de maternelle, vers l’âge de trois ans, à l’occasion du passage du photographe scolaire. Pour bien composer sa photo, le photographe doit placer les enfants sur le banc en fonction de leurs tailles.

Pour cela, le photographe passe en revue les enfants à la recherche du plus petit. Une fois trouvé, il le place sur le banc. Il réitère cette opération sur les enfants restant en plaçant à chaque fois l’enfant sélectionné à la prochaine place disponible sur le banc. L’algorithme se termine lorsqu’il ne reste plus d’enfant. Si vous avez bien suivi, vous aurez compris que le dernier enfant à être sélectionné, et donc à être placé sur le banc, est mécaniquement le plus grand.
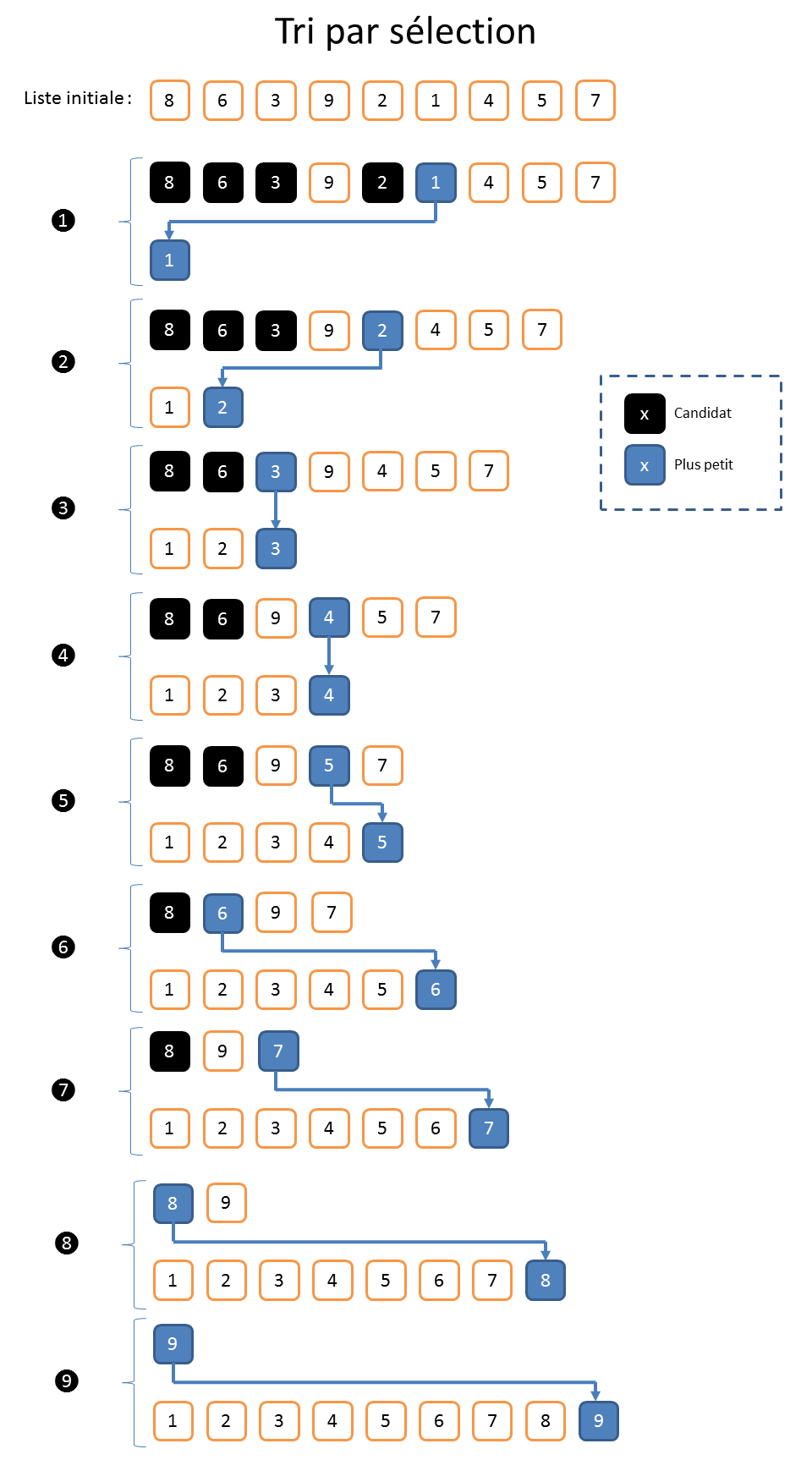
Cet algorithme aurait pu s’appeler le « tri du photographe », mais on le trouve dans la littérature sous le nom de « tri par sélection ».
Dans la suite, on notera « n » le nombre d’éléments dans la liste à classer. Dans l’exemple, « n » correspond donc au nombre d’enfants dans la classe. À titre d’illustration, disons qu’il y en a dix-huit (cf. dessins). Pour sélectionner le plus petit, le photographe doit donc passer en revue les 18 élèves, ce qui nécessite de faire 17 comparaisons. Pour le deuxième, il reste 17 élèves à comparer, nécessitant 16 comparaisons. Pour le troisième il faudra faire 15 comparaisons, et ainsi de suite… Au final, le photographe va donc faire « 17+16+15+…+1 » comparaisons, ce qui est un peu long à calculer. Heureusement, on fait un peu de math au lycée. Ça peut se factoriser à l’aide de la formule « n*(n-1) /2 », ce qui donne « 153 » comparaisons pour une classe de dix-huit bambins.
À la fin de la journée, le photographe doit donc avoir un sacré mal de tête. Et encore, il s’agit d’une classe relativement peu chargée. En école d’ingénieur, nous étions 150 dans ma promotion. Le photographe devrait donc faire plus de onze mille (11175) comparaisons pour préparer sa photo à l’aide du tri par sélection : autant dire qu’il y passerait la journée. Sans vendre la mèche, on devine déjà que le « tri par sélection » n’est pas réputé pour être très efficace.
Tri par insertion
Lorsqu’on est enfant, il y a un autre algorithme de tri qu’on apprend (ou découvre) assez vite. C’est celui que les joueurs de cartes utilisent pour organiser leurs mains. Le joueur pioche la carte qui est en haut du tas et la place (l’insère) à la bonne position dans la main. Cet algorithme se nomme le « tri par insertion ».
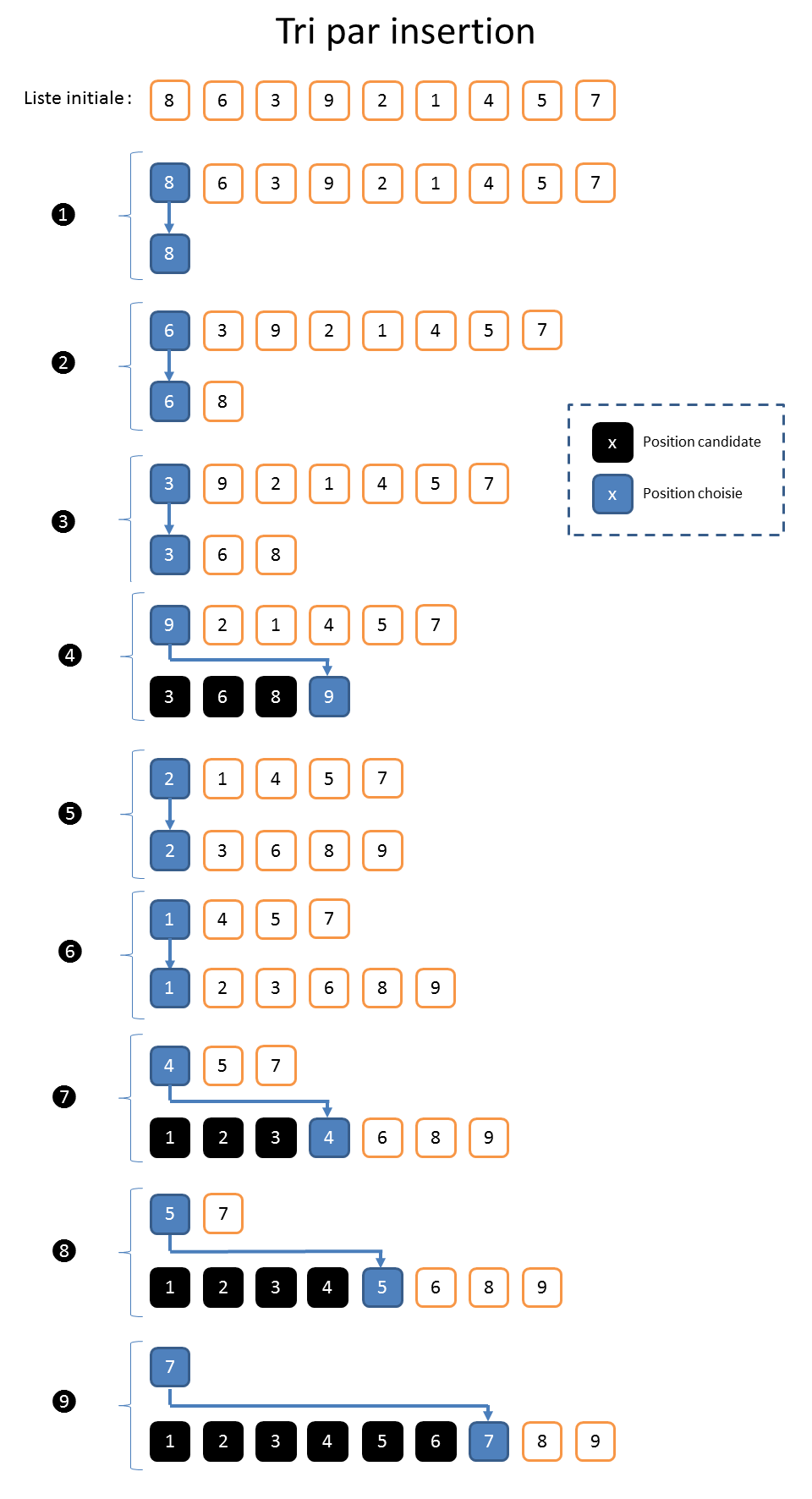
En première approche, le « tri par insertion » est donc l’inverse du « tri par sélection ». Il est toutefois un peu plus efficace. À titre d’illustration, prenons de jeu de la Belote[3] dans lequel chaque joueur reçoit huit cartes. Ici « n » vaudra donc « 8 ». Pour la première carte, il n’y a rien à faire puisque la main est vide. Pour la deuxième carte, il y a une comparaison à faire avec l’unique carte déjà en main pour savoir si elle doit aller à gauche ou à droite. Pour la troisième carte, il y aura « au maximum » deux comparaisons à effectuer. Il est important de comprendre qu’on arrête de faire des comparaisons dès que la bonne position est identifiée. On fait ainsi tant qu’il reste des cartes à piocher.
Au final, et dans le « pire des cas », on fera donc « 1+2+…+7 » comparaisons, soit « 28 » au total. C’est la même formule (à l’envers) de calcul que pour le « tri par sélection » et ce n’est donc pas mieux. En revanche, dans le « meilleur des cas » où le joueur pioche les cartes dans l’ordre idéal (ie. triées dans l’ordre croissant ou décroissant selon qu’on insère par la tête ou par la queue), il n’y aura que 7 comparaisons. Et bien entendu, plus le nombre « n » est grand et plus la différence est sensible.
Complexité
Comme vous l’avez surement déjà deviné, le nombre total d’opérations à effectuer pour « dérouler » un algorithme est un critère majeur pour dire si l’algorithme est efficace. Cela permet surtout de comparer l’efficacité de deux algorithmes et de choisir le plus adapté.
Il est relativement « simple » de dénombrer « précisément » le nombre d’opérations nécessaires pour « dérouler » un algorithme de tri lorsque le nombre d’éléments « n » dans la liste est petit. Par exemple, on a vu qu’il faudra réaliser « 153 » comparaisons pour trier « 18 » enfants à l’aide du « tri par sélection ». Le même algorithme nécessite de réaliser « 11.175 » comparaisons pour trier une classe de « 150 » élèves, et « 499.500 » pour trier les mille employés d’une PME. Et si vous vouliez trier les « 81.338 » spectateurs d’un match de foot au Stade de France, il faudrait « 3.307.894.453 » comparaisons.
Ces exemples mettent deux choses en évidence. Premièrement, la quantité d’opérations nécessaire au déroulement du « tri par sélection » croît rapidement lorsque le nombre « n » d’éléments dans la liste augmente. Deuxièmement, il n’est pas nécessaire d’avoir une grande précision sur des chiffres aussi importants. Quand on réalise « 3.307.894.453 » comparaisons, on n’est plus à une comparaison près, ni à dix, ou cent, ou même cent millions. D’ailleurs on aurait pu se contenter de dire qu’il fallait « environ trois milliards » d’opérations. Ce qui compte, avec des valeurs si conséquentes, c’est d’avoir un « ordre de grandeur », même vague. C’est ce qu’on va appeler la « complexité » d’un algorithme.
En fait, il n’est pas possible de discuter des tris sans parler de « complexité ». Ce mot à lui seul est synonyme de cauchemars pour bien des étudiants en école d’info. Et pour ma part, je dois avouer que j’ai mis longtemps à en comprendre les tenants et les aboutissants. Je me propose donc de vous l’expliquer simplement, en prenant quelques raccourcis. Ne vous inquiétez pas si tout n’est pas clair, ça va se clarifier au fur et à mesure.
La complexité d’un tri de « n » éléments se note avec un « omicron » : dites « grand O ». Par exemple, la complexité du « tri par sélection » sera en « O(n*(n-1) /2 ) », où « n*(n-1) /2 » est la formule qu’on avait utilisée un peu plus tôt. Comme on s’intéresse à des valeurs importantes et qu’on ne veut qu’un « ordre de grandeur », on considèrera que cette « complexité » peut se « simplifier » en « O(n*(n-1)) », qui peut elle-même se simplifier en « O(n²) ». On dira que l’algorithme du « tri par sélection » est de « complexité quadratique » en « O(n²) ».
Pour faire simple, quand vous multipliez par « 10 » le nombre « n » d’éléments, vous multipliez par « 100 » le nombre d’opérations à réaliser lorsque vous utilisez un algorithme de tri en « O(n²) ». Dit comme ça, ce n’est pas très impressionnant alors essayons d’associer cela avec des durées pour voir à quel point c’est mauvais. Disons pour simplifier qu’une opération prenne une nanoseconde (ns) en moyenne (ce qui est très optimiste).
| Nombre d’éléments « n » | Nombre d’opérations pour un tri en « O(n²) » | Durée pour un tri en « O(n²) » |
| 10 | 100 | 100 ns |
| 100 | 10 000 | 10 us |
| 1 000 | 1 000 000 | 1 ms |
| 10 000 | 100 000 000 | 100 ms |
| 100 000 | 10 000 000 000 | 10 s |
| 1 000 000 | 1 000 000 000 000 | 16 min 40 s |
| 10 000 000 | 100 000 000 000 000 | 27 heures |
| 100 000 000 | 10 000 000 000 000 000 | 115 jours |
| 1 000 000 000 | 1 000 000 000 000 000 000 | 31 ans |
Alors que le tri de « 10 » éléments prendra seulement « 100 » nanosecondes à l’aide d’un algorithme en « O(n²) », il faudra « 10 » microsecondes pour une centaine d’éléments et carrément une milliseconde pour mille. Et ces temps augmentent encore quand le nombre d’éléments augmente. Ça augmente même très vite. Pour un milliard d’éléments, ce qui est un chiffre tout à fait raisonnable pour un programme informatique, on aura besoin d’un tiers de siècle. Autant dire que les données seront périmées depuis longtemps quand l’algorithme aura fini son travail. L’ordinateur sera peut-être même déjà passé à la poubelle. Et je ne vous parle même pas de la facture d’électricité qu’on aurait tendance à oublier (coût en énergie, en ressource naturelle, en entretien et en Euro).
Pour bien réaliser ce que ça représente, prenons un exemple plus concret. Pour trier la population mondiale[4], soit un peu plus de sept milliards de personnes (au début de l’été 2014), il faudrait plus d’un millier et demi d’années (1655 ans environ). Pour que le tri soit fini au moment où vous écoutez/lisez ce dossier, il aurait donc fallu le commencer en l’an 350 de notre ère, soit plus d’un siècle avant le début du moyen âge (476 à 1453).
On parle de complexité en se plaçant dans la situation la plus défavorable pour l’algorithme. Ça permet en quelque sorte de majorer. On peut aussi se placer dans le cas le plus favorable ou dans le cas moyen. Par exemple et sans plus d’explications, le « tri par insertion » sera de « complexité linéaire » en « O(n) » dans le cas le plus favorable et en « O(n²) » dans les cas moyens et défavorables.
Bon, je ne vais pas vous embêter plus que ça avec cette histoire de complexité (pour l’instant). Les informaticiens qui écoutent diront que j’ai mis de côté la moitié des choses (gestion de la mémoire, déplacements, permutations, création d’objets, flux, etc.), mais je pense sincèrement que l’essentiel y est, pour l’instant 😉
Comment faire mieux ?
On devine qu’il va falloir trouver comment faire mieux, notamment en utilisant des algorithmes beaucoup plus rapides. Rassurez-vous, je ne vais pas vous présenter tous les algorithmes de tri qui existent. Je vais me limiter aux plus connus en insistant sur leurs points forts et leurs faiblesses.
Tri à bulle (Bubble Sort)
Le tri à bulle est certainement celui qu’on apprend à programmer en premier en école d’informatique, avant même le « tri par sélection » et le « tri par insertion ». Pour effectuer un « tri à bulle », il faut parcourir la liste en permutant les éléments contigus qui ne sont pas dans le bon ordre. Par exemple, si je trouve « 9 » dans la case « 4 » et seulement « 2 » dans la case « 5 », alors j’échange leurs positions. Quand c’est fini, l’élément le plus grand se retrouve donc en queue de liste. Cet élément est arrivé à sa bonne position, mais le reste de la liste est encore potentiellement en désordre. On recommence autant de fois qu’il y a d’éléments dans la liste, ce qui fait donc à chaque fois remonter le plus grand élément restant.
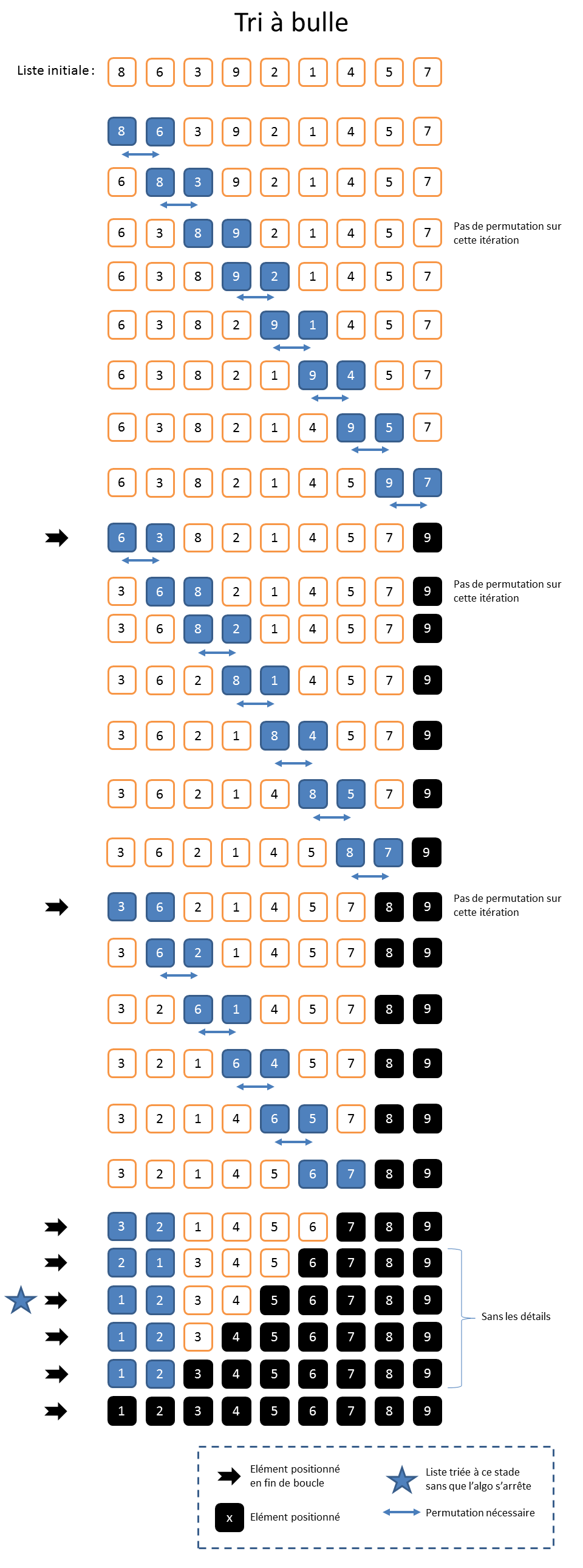
Le nom du « tri à bulle » vient du fait que les plus gros éléments remontent comme des bulles dans une flute de champagne. D’ailleurs, on n’utilise jamais le « tri à bulle », car les bulles remontent très lentement.
Pour une liste dans laquelle le nombre d’éléments « n » est de « 9 », on fera « 8 » (ie. « n-1 ») comparaisons pour mettre le plus grand élément à sa bonne position. Et on va répéter cela « 8 » fois également, ce qui nécessitera donc « 64 » comparaisons. La complexité associée au « tri à bulle » sera donc en « O((n-1)²) » qu’on simplifiera en « O(n²) ».
On peut améliorer l’algorithme de base. En effet, à chaque passage, un élément supplémentaire se retrouve à sa place définitive. Il n’est donc plus nécessaire de l’inclure dans les comparaisons suivantes.
On n’aura alors besoin que de « (n-1)*n/2 » comparaisons, soit « 36 » comparaisons pour une liste de « 9 » éléments. La complexité restera toutefois en « O(n²) », le multiplicateur « ½ » ne changeant rien à l’histoire pour les grandes valeurs, comme on l’a déjà vu.
À titre personnel, je dois avouer que j’ai beaucoup d’affection pour le « tri à bulle », même en sachant que ce n’est pas le meilleur.
Tri rapide (Quick Sort)
S’il y a un algorithme de tri dont vous avez forcément entendu parler à la machine à café, c’est bien le « Quick sort ». C’est l’un des algorithmes les plus utilisés et certainement celui qui présente le plus de variantes. Le « Quick Sort », aussi appelé « tri rapide », fait partie de la famille d’algorithme dont le fonctionnement repose sur le principe « diviser pour régner ».
Pour réaliser un « tri rapide », on doit choisir un élément dans la liste, qu’on appelle « pivot ». On divise ensuite la liste en deux sous-listes. La première, à gauche, contient les éléments inférieurs au pivot. La seconde, à droite, contient les éléments supérieurs au pivot.
On reproduit alors récursivement ce choix du pivot et la division sur les listes de gauche et de droite précédemment construites jusqu’à n’avoir que des sous-listes de zéro ou un élément. Pour finir, il suffit de rassembler les éléments de toutes les sous-listes dans l’ordre gauche-droite.
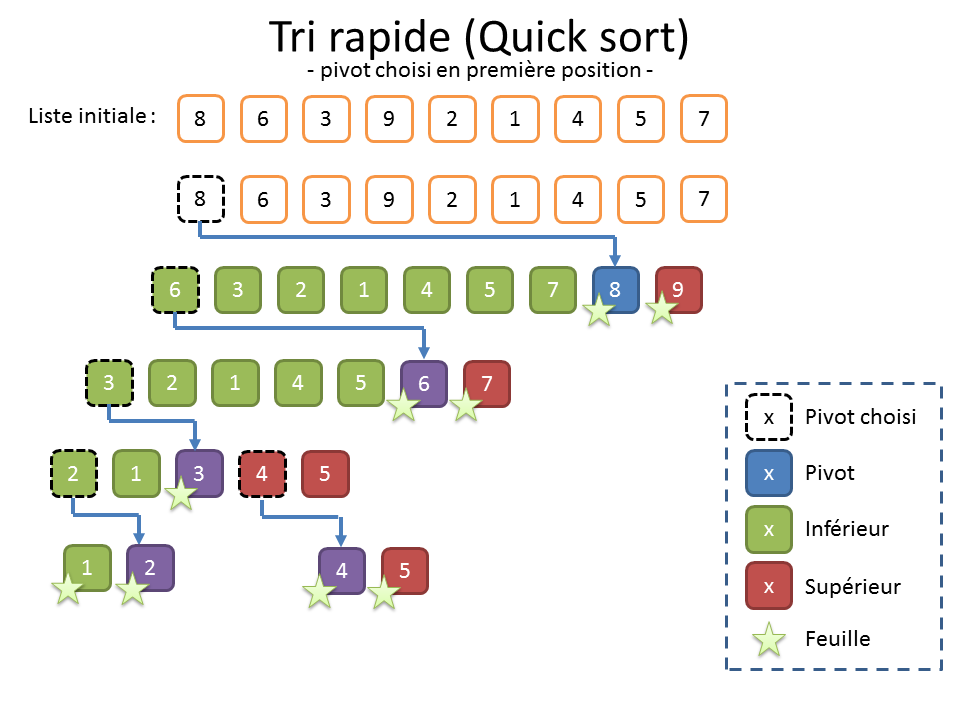
La grosse difficulté du « Quick sort » réside dans le choix du bon pivot, le risque étant de déséquilibrer les sous-listes qu’on va construire. Quand on n’a pas de meilleure idée et faute de mieux, on peut prendre le premier élément (cf. illustration ci-dessus).
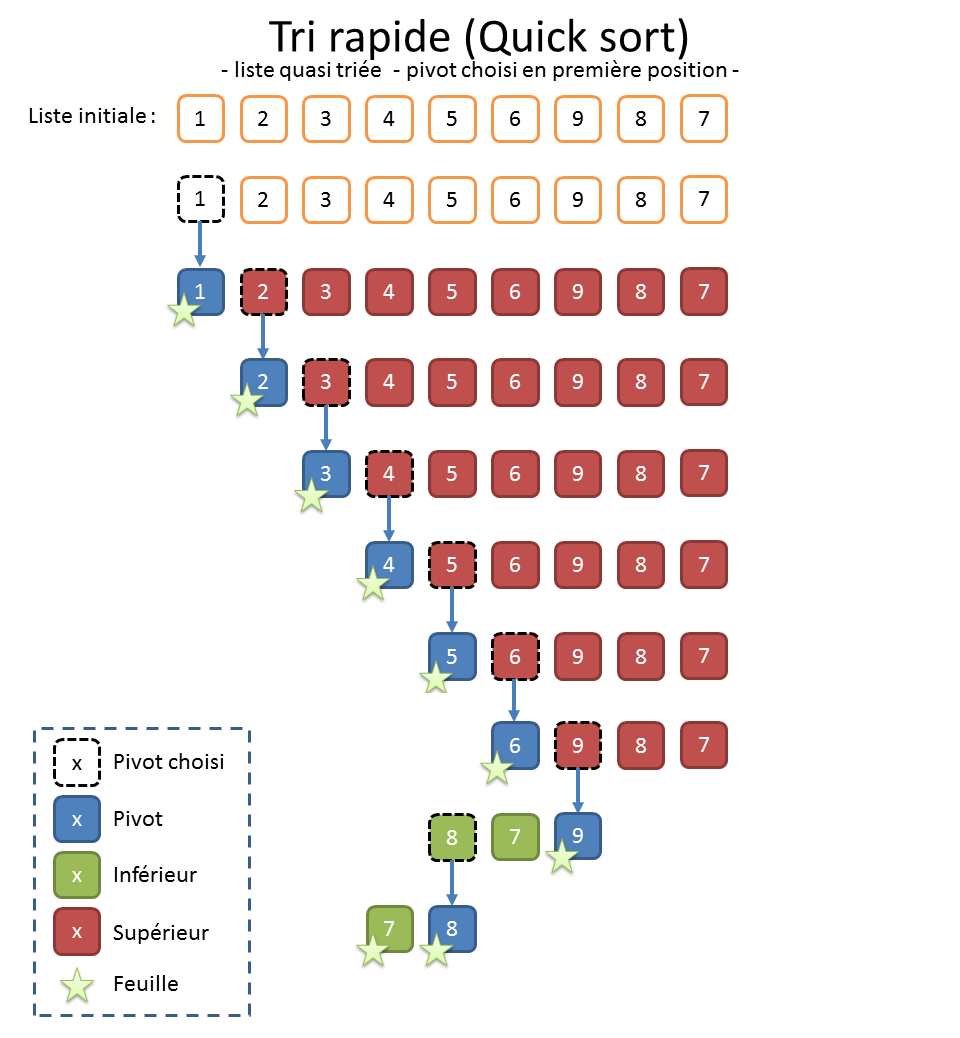
Lorsqu’on soupçonne que les données sont déjà à peu près triées et que le choix du pivot en première position provoquera un déséquilibre (cf. illustration ci-dessus), on peut aussi préférer choisir le pivot au milieu (cf. illustration ci-dessous).
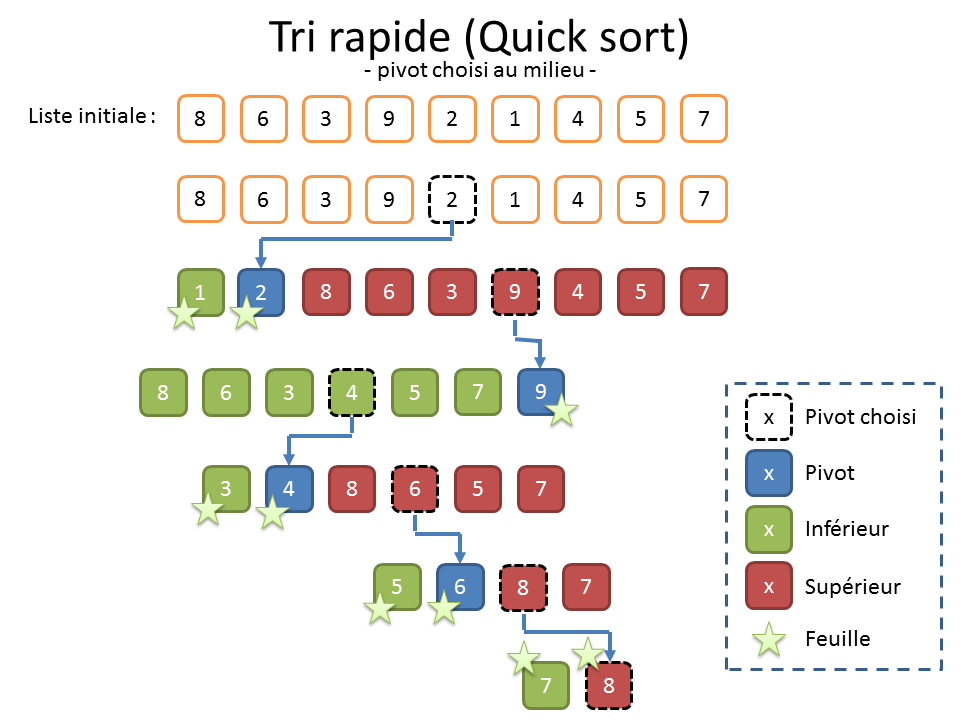
Et quand on n’a aucune information sur les données, on peut également choisir le pivot de manière aléatoire (cf. illustration truquée ci-dessous). Un mathématicien comme Nicotupe vous dirait que ça permet de maximiser « l’espérance » que ça se passe bien. Personnellement, je n’aime pas trop cette solution. Elle donne souvent de bons résultats, mais le déroulement de l’algorithme est alors aléatoire. Or, en bon informaticien, je n’aime pas trop quand c’est non reproductible. En outre, ça laisse la porte ouverte pour toutes les combinaisons où ça peut mal tourner. Or, en informatique, comme l’énonce la loi de Murphy[5], tout ce qui peut mal tourner va mal tourner.
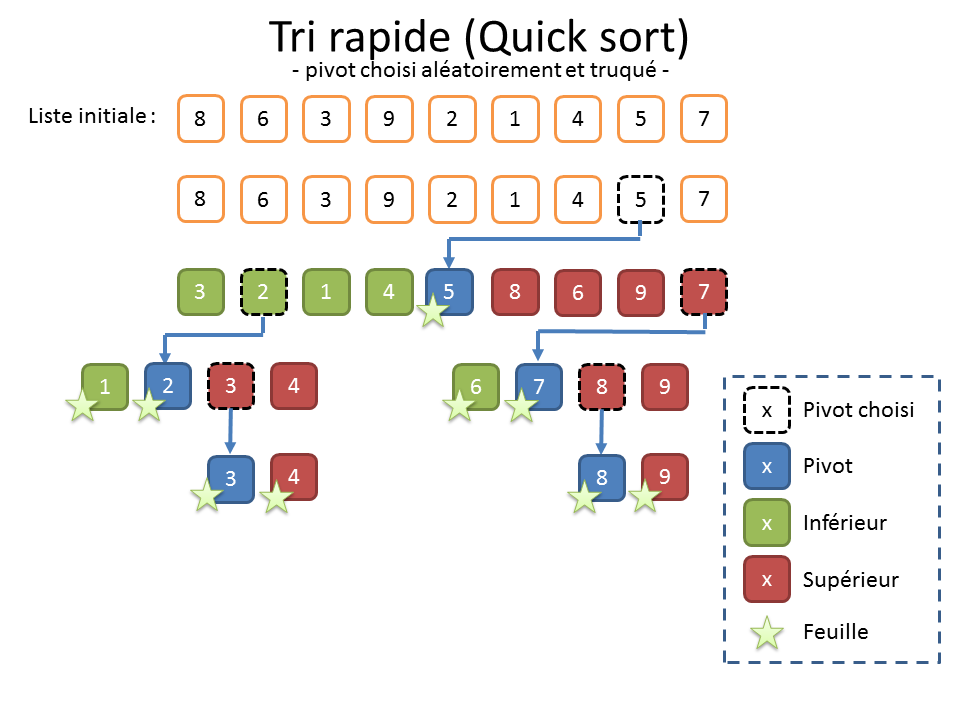
Comme son nom l’indique, le « Quick Sort » a la réputation d’être rapide, ce qui est mérité, mais parfois un peu usurpé. Pour le comprendre, il va encore falloir parler de complexité.
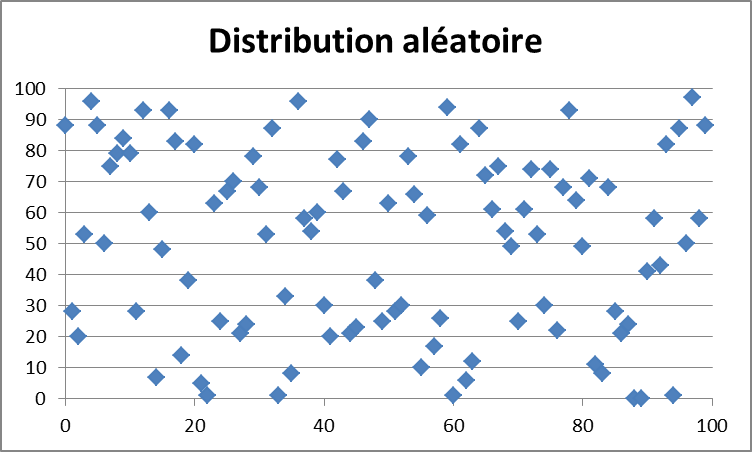
Dans le cas favorable où les éléments sont uniformément distribués, c’est-à-dire bien mélangées (cf. illustration ci-dessus), l’algorithme produit un arbre équilibré avec « 2 » sous-listes de taille « n/2 » à chaque appel récursif, soit « n » opérations à chaque étape (une étape est un nœud de l’arbre ou une feuille).
À l’étape « 1 », on aura donc « 2 » sous-listes. À l’étape « 2 », on aura « 2*2 = 22 » sous listes. À l’étape « 3 », on aura « 2*2*2=23 » sous listes, et ainsi de suite. À l’étape « p », on aura « 2*2*2*…*2=2p » sous listes. L’algorithme récursif s’arrête lorsqu’on arrive à un seul élément. S’il faut « p » étape pour cela, on pourra donc dire que « n=2p ». La fonction mathématique qui permet de calculer la valeur de « p » quand on connait « n » est le « logarithme de n en base 2 » qu’on note « log2(n) » ou « lg(n) » en raccourci. Au final, la complexité du « tri rapide » sera donc en « O(n lg n) ».
Dans le cas défavorable où les éléments sont déjà triés (cf. illustration ci-dessus), l’algorithme produit un arbre complètement déséquilibré, ressemblant à une longue tige tordue et ne permettant de trouver la position que d’un seul élément à chaque étape. On aura donc une complexité équivalente à celle du « tri par sélection » en « O(n²) ».
Si on raisonne de nouveau en terme de durée, on se rend compte qu’il y a une véritable différence entre un algorithme de tri en « O(n lg n) » et un autre en « O(n²) ».
| Nombre d’éléments « n » | Durée pour un tri en « O(n lg n) » | Durée pour un tri en « O(n²) » | |
| 10 | 33 ns | 100 ns | |
| 100 | 664 ns | 10 us | |
| 1 000 | 10 us | 1 ms | |
| 10 000 | 132 us | 100 ms | |
| 100 000 | 1,6 ms | 10 s | |
| 1 000 000 | 20 ms | 16 min 40 s | |
| 10 000 000 | 233 ms | 27 heures | |
| 100 000 000 | 2,5 s | 115 jours | |
| 1 000 000 000 | 29 s | 31 ans | |
| Population mondiale | 4 min | 1 655 ans | |
Souvenez-vous. Un peu plus tôt, je vous ai dit qu’il fallait « 100 ns » pour trier une liste de « 10 » éléments à l’aide d’un algorithme en « O(n²) » et d’un bon ordinateur. Si on se place dans un cas en « O(n lg n) », il ne faudra plus que « 33 ns ». Bon, la différence ne saute pas aux yeux. Pour un million d’éléments, on passe de « 16 minutes » à « 20 ms », ce qui reste encore dans les limites du temps réel. Et pour trier la population mondiale, on passe de « 1655 ans » à seulement « 4 minutes ».
Notez qu’il existe une optimisation du « Quick sort » assez contre-intuitive. Elle préconise de mélanger la liste avant de la trier. L’idée est de se rapprocher de la complexité en « O(n lg n) » du cas favorable où la liste est complètement mélangée, quitte à dépenser un « O(n) » à préparer la liste.
Tri fusion (Merge Sort)
Dans la grande famille des tris reposant sur le principe « diviser pour régner », on trouve le « tri Fusion ». À mon sens, le « tri Fusion » est au « tri rapide » ce que le « tri par insertion » est au « tri par sélection ». Dans cette famille de tri, on travaille toujours en trois phases. D’abord on divise. Ensuite on règne. Et pour finir, on réconcilie (fusionne). Alors que, pour le « Quick Sort », tout se fait à la construction de l’arbre, pour le « tri fusion », la partie intéressante se situe lors de la phase de réconciliation.
Pour réaliser un « tri fusion », on commence par diviser la liste à trier en deux sous-listes de même taille. On réitère récursivement cette opération jusqu’à n’avoir que des listes d’un seul élément. Cela produit donc un arbre à peu près équilibré. On remonte ensuite dans l’arbre en fusionnant les sous-listes à chaque étape. Pour cela, on prend le plus petit élément qui se présente en tête des deux sous-listes à fusionner et on recommence tant qu’il reste des éléments. Quand on revient à la « racine » de l’arbre, la liste est triée.
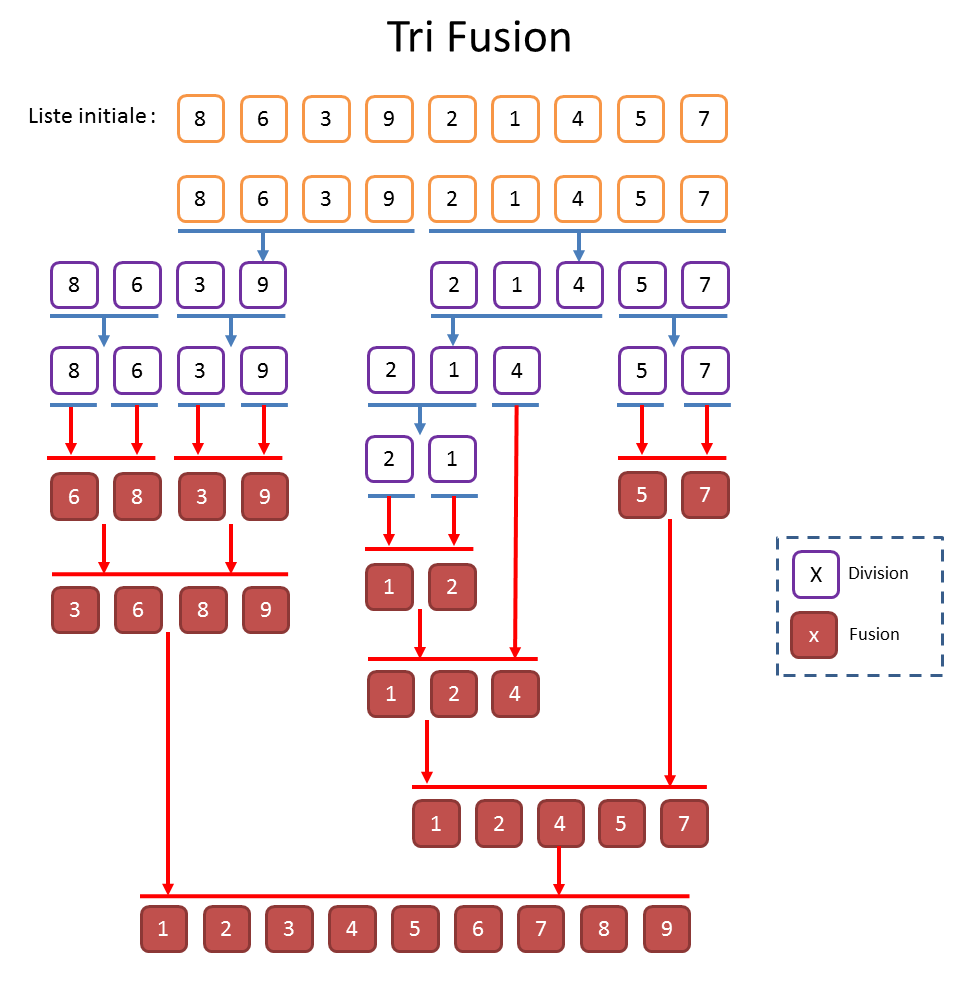
Le coût des divisions récursives est quasi gratuit. Il est systématique et ne demande de réaliser aucune comparaison entre les éléments. Si vous avez compris ce qu’on avait dit pour la complexité du « quick Sort », vous avez certainement déjà deviné que la complexité du « tri fusion » sera en « O(n lg n) » dans tous les cas puisqu’on force la production d’un arbre équilibré.
Tri par interclassement monotone
À l’époque où on utilisait encore des bandes magnétiques, le « tri par interclassement monotone » avait ses adeptes. Comme son nom l’indique, ce tri se base sur la « monotonie » dans l’ordonnancement des éléments d’une liste.
Pour dérouler cet algorithme, on répète deux phases jusqu’à ce que ce soit trié, en utilisant des bandes magnétiques ou des zones mémoire temporaires « A » et « B ».
Durant la phase « 1 », on recopie les éléments de la bande magnétique initiale « I » vers la bande « A » tant que les éléments sont croissants. On copie vers la bande « B » dès qu’ils sont décroissants. On continue sur la bande « B » jusqu’à ce qu’il y ait une décroissance en reprenant alors sur la bande « A ». Pour simplifier, on recopie les éléments sur une bande et on change de bande à chaque décroissance.
Durant la phase « 2 », on fusionne les bandes « A » et « B » sur la bande « I » en copiant toujours le plus petit élément en tête des bandes.
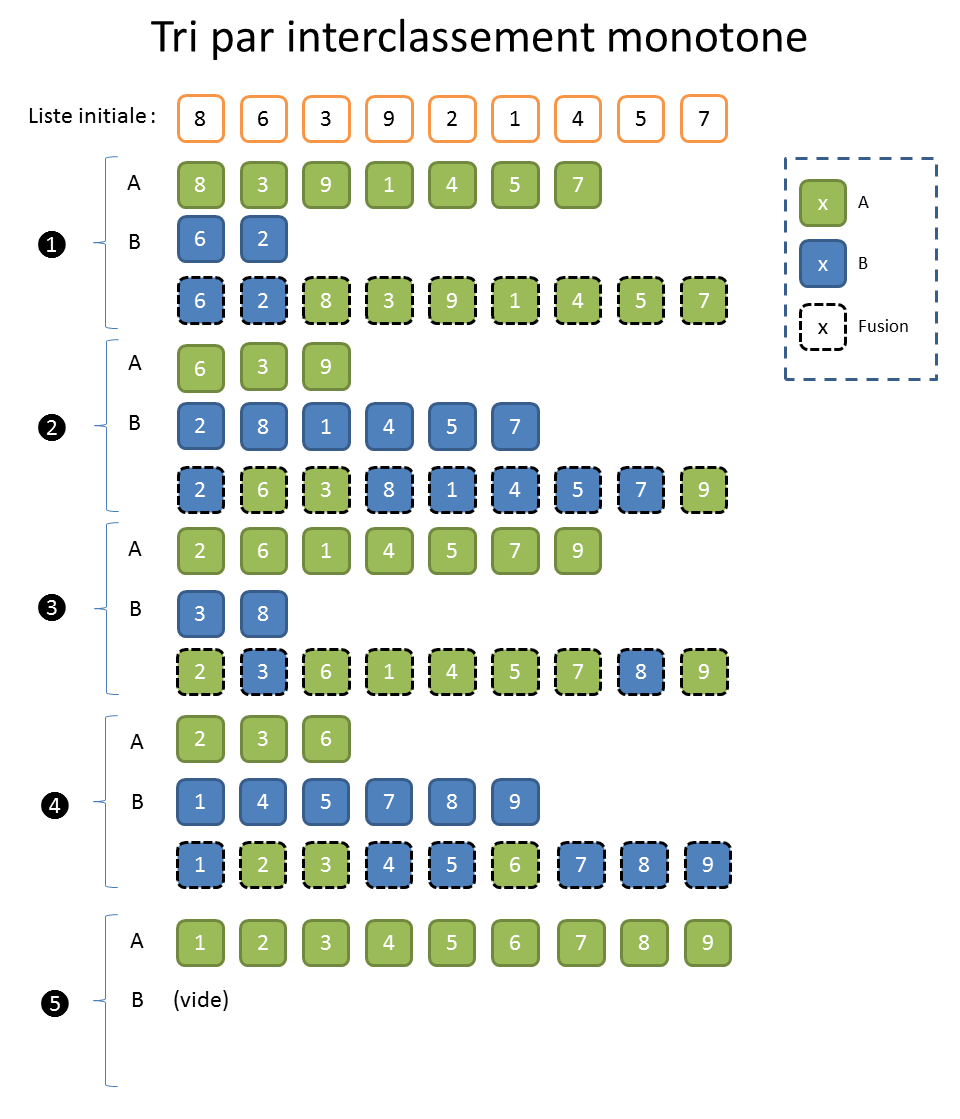
Je vous vois venir ; on n’en est plus à l’époque des bandes magnétiques. Cela dit, le temps de transfert d’un tableau de la mémoire centrale aux caches CPU, comparé à celui d’une liste chaînée, dont les éléments sont dispersés dans la mémoire, se pose exactement dans les mêmes termes. Et puis, on peut utiliser ce type de tri pour trier des gros fichiers dans un environnement contraint en mémoire puisqu’il n’y a besoin que d’ouvrir deux flux de sortie et un d’entrée, ainsi qu’une paire de variables.
Ce tri fonctionne relativement bien sur des listes mélangées. Son fonctionnement est presque magique quand on s’amuse à le dérouler sur papier. Mais c’est avec les listes en partie triées qu’il dévoile tout son potentiel. La connaissance, même faible, qu’on peut avoir à l’avance sur les données est donc très importante.
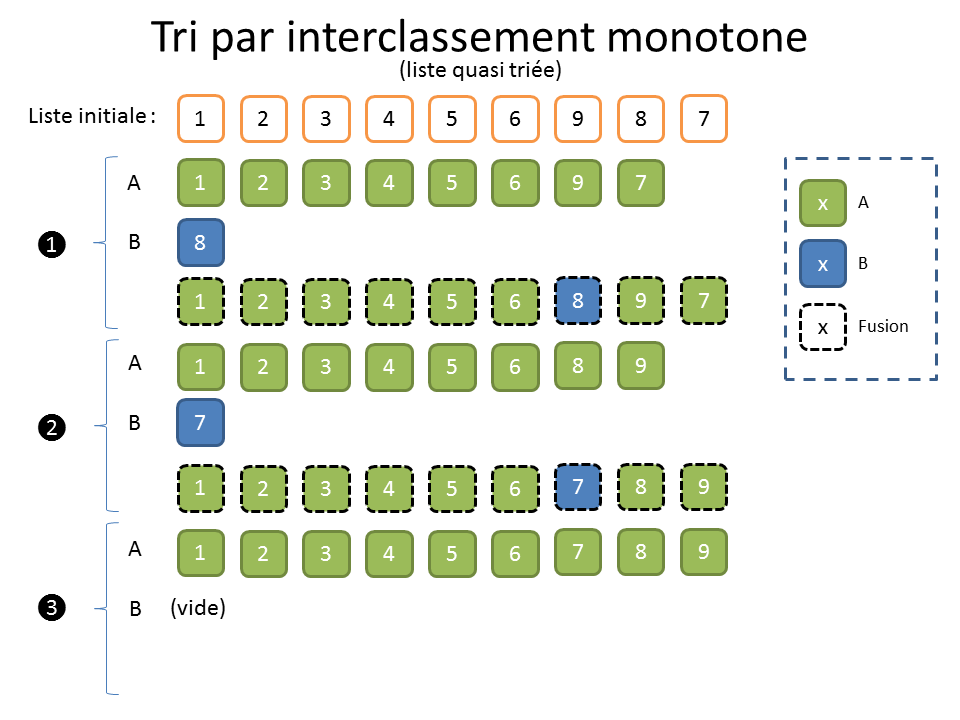
Pour la complexité, très sommairement, il y a donc « n » lectures et « n » écritures par phases. La longueur des sous-suites monotones est TRES grossièrement « 2 » puis « 4 » puis « 8 », bref, on va avoir « lg(n) » étapes (même raisonnement que pour un arbre). C’est assez approximatif, mais disons que dans le pire des cas, c’est en « O(n lg n) » et que, dans le cas de listes partiellement triées, c’est quasi linéaire en « O(n) ».
Je vous invite à lire mon blog[6] pour en savoir un peu plus sur le « tri par interclassement monotone » et découvrir quelques unes de ses variantes.
Positionnement direct (tri sans comparaison)
Parfois, on connait à l’avance la composition de la liste. Imaginons par exemple que la liste soit composée des membres de la Suite de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21…) que Mathieu nous avait présentée à l’occasion d’un dossier[7] sur le nombre d’or. Avec cette information en poche, on ne va pas perdre notre temps à trier la liste puisque chaque élément porte intrinsèquement sa position. Par exemple, on sait que l’élément « 13 » doit aller à la position « 6 ».
La puissance des machines là-dedans
D’après la loi de Moore[8], la puissance des processeurs double tous les 18 mois. Les traitements doivent donc aller deux fois plus vite. C’est vrai, mais c’est sans compter que quantité de données augmente également. Imaginons qu’elle ne fait que doubler sur la même période. Instinctivement, on se dit que ça double la quantité de calcul et que sera compensé par l’augmentation de puissance, mais c’est trompeur.
Pour le comprendre, je vais devoir vous infliger encore un petit peu de math. Prenons un algorithme en « O(n²) » comme le « tri par sélection ». On double la quantité « n » de données et on divise par deux le temps de calcul pour que ce soit cohérent avec l’augmentation de puissance. On aura donc « (2n)²/2 = 4n²/2 = 2n² », ce qui est évidement plus grand que « n² ».
Doubler la puissance ne suffit donc pas à compenser l’augmentation du volume de données et on ne peut donc pas se reposer sur l’amélioration des matériels. Il faut donc choisir avec attention son algorithme et l’adapter à son contexte.
D’ailleurs, les constructeurs de processeurs ne font plus la course à la vitesse ; on n’essaie plus d’avoir des Méga Hertz, pour plein de bonnes raisons technologiques. À la place, on préfère multiplier le nombre de cœurs. L’avenir des tris complexes passe donc sans aucun doute par le parallélisme offert dans les processeurs multicœurs. Des algorithmes comme le « Quick Sort » seront les premiers à en profiter.
Conclusion
Alors, c’est quoi, le meilleur tri ? En fin d’année, Benny Scetbun répondait aux questions[9] de Nico à propos de l’école « 42 ». Dans cette interview, il explique que le « Quick Sort » était autrefois considéré (c’est malheureusement encore enseigné à l’école) comme le meilleur algorithme de tri. Il précise toutefois que cela dépend du contexte.

En effet, les listes qu’on doit manipuler sont statistiquement déjà ordonnées, tout simplement parce qu’on les a déjà triées la veille, l’avant-veille, etc. Les seuls éléments mal ordonnés sont ceux en queue (cf. illustration ci-dessus), qu’on a ajoutés depuis le dernier tri. Du coup, le « Quick sort » est un bon algorithme en théorie, mais un mauvais dans la pratique. L’appliquer sur une liste déjà en partie triée le place dans son pire cas de complexité en « O(n²) ».
Notez que la bonne stratégie à appliquer dans cet exemple aurait été de ne trier que les données ajoutées récemment puis d’employer un algorithme similaire au « tri par insertion », que je vous ai présenté au début de ce dossier, pour les positionner correctement.
Combinaisons de tri
Les études des complexités servent d’une part à martyriser les étudiants en école d’info, et d’autre part à savoir quand et comment utiliser les algorithmes. Une des conséquences est qu’il peut être intéressant de combiner plusieurs algorithmes.
Par exemple, la méthode de tri incluse dans le langage en Java (mon langage de prédilection) garantit un tri stable avec des performances en « O(n lg n) », ce qui est relativement honnête. Java utilise une combinaison d’algorithmes en fonction de la taille des listes. En dessous de « 7 » éléments, ça utilise un « tri par insertion ». Entre « 7 » et « 40 » éléments, ça emploie un « Quick Sort avec une médiane de trois ». Pour les listes plus grosses, ça utilise un « Quick Sort avec une médiane de neuf ». Les « médianes » désignent des variantes classiques sur le choix du pivot. Notez que les langages évoluent. Ainsi, depuis la version 7, Java utilise un « Quick sort avec double pivot » pour les listes de plus de « 7 » éléments.
Tri ou presque
La course au meilleur algorithme est un sujet vraiment important pour certaines entreprises. Un bon tri peut même s’apparenter à un avantage concurrentiel sérieux. Dans certaines situations, on n’a pourtant pas réellement besoin d’un résultat parfait.

Reprenons l’exemple du photographe avec lequel on a commencé ce dossier. Il doit trier les enfants selon leurs tailles pour bien composer la photo de classe. Mais en réalité, il ne va pas s’amuser à mesurer chaque élève. Il fait ça au jugé. Et s’il s’est un peu trompé dans l’ordre final (cf. illustration ci-dessus), on pourrait parier que ça ne se verra pas.
Tri du dormeur
Pour finir, et parce que ce qu’il est déjà tard, je voudrais vous présenter un algorithme de circonstance puisqu’il s’agit du « tri du dormeur ». Ce tri a un nom qui me fait rigoler, d’autant qu’il le porte bien, car son principe de fonctionnement consiste précisément à dormir…
Pour chaque élément de la liste, on lance un processus indépendant (un thread), qui se met en sommeil (pause) pour une durée égale à la valeur de l’élément. Par exemple, pour la valeur « 13 », le processus dort durant « 13 » millisecondes. Lorsque le processus se réveille, on ajoute directement son élément (« 13 » dans l’exemple) en queue d’une seconde liste. L’air de rien, ça marche super bien (mille éléments traités en une seconde) pour des listes dont les éléments n’ont pas des valeurs trop élevées. Le « tri du dormeur » nécessite toutefois une quantité astronomique (pour ne pas dire « infiniment grande ») de mémoire.
Vraie conclusion
En fait, il n’existe pas d’algorithme de tri qu’on puisse considérer comme le meilleur. On pourrait généraliser cela en informatique par le fait qu’il n’y a pas de solution magique qui marche dans tous les cas. Par contre, on connait des réponses qui fonctionnent relativement bien dans des situations spécifiques.
Quand on est développeur, il est indispensable de savoir comment le langage (Java, Lisp…), la base de données (Oracle, MySql, Mongo…) ou encore le progiciel (Kyriba, Excel…) trie les données. Il faut surtout savoir quand utiliser les mécanismes fournis et quand les fuir.
Bref. On arrive à la fin de ce dossier, pour de vrai. S’il y a quelque chose à retenir, c’est qu’il n’est pas si trivial de trier des données, en particulier lorsque les quantités sont conséquentes. Et surtout, il n’y a pas de solution miracle qui marche dans tous les cas.
[1] Algorithme sur Wikipedia : http://fr.wikipedia.org/wiki/Algorithme [2] Episode n°82 de Podcast Sciences, intitulé « Les algorithmes ou l’histoire de la recette de cuisine » : https://www.podcastscience.fm/emission/2012/04/18/podcast-science-82-les-algorithmes-ou-lhistoire-de-la-recette-de-cuisine/ [3] La belote se joue à 4 joueurs avec un paquet de 32 cartes, soit 8 pour chaque joueur. [4] Population mondiale estimée au 1er juillet 2014 : 7 226 376 025 personnes. [5] http://fr.wikipedia.org/wiki/Loi_de_Murphy [6] http://blog.developpez.com/todaystip/p11899/dev/tri-par-insertion-monotonie [7] Dossier : https://www.podcastscience.fm/dossiers/2011/03/17/la-suite-de-fibonacci-nombre-d-or/ [8] Loi de Moore : http://fr.wikipedia.org/wiki/Loi_de_Moore [9] Interview de Benny Scetbun : http://nicotupe.fr/Blog/2013/09/42-interview-de-benny-scetbun/



