Disclaimer :
Ouh-la, cet article du tout début de notre site est un peu étrange ! On s’était apparement laissé un peu avoir par la nombre-d’or-mania et, avec quelques années de recul, on est pas extrêmement fier de son contenu. On vous propose donc plutôt d’aller voir ce billet de l’excellent blog Choux romanesco, Vache qui rit et intégrales curvilignes intitulé Le plus doré de tous les nombres qui en parle bien mieux que nous le faisons ici.
L’équipe de Podcast Science
Dossier de Mathieu dans l’épisode #28.
La suite de Fibonacci doit son nom au mathématicien italien Leonardo Fibonacci qui a vécut au XIIème et XIIIème siècle. Il est connu pour avoir introduit et popularisé en Europe et en Occident la numérotation indo-arabe qui a remplacé pour les calculs la notation romaine peu pratique aux opérations arithmétiques.
Mais il est aussi connu pour avoir mis en évidence une suite mathématique qui porte désormais son nom. Dans la suite de Fibonacci, il n’est pas nécessaire de mémoriser chacun des termes ou nombres de la suite (qui est d’ailleurs infinie). Il suffit de se rappeler sa règle de construction: à l’exception des deux premiers, chaque terme de la suite est égal à la somme des deux termes qui le précèdent immédiatement, dit autrement il s’agit d’une suite de nombres dans laquelle tout nombre (à partir du troisième) est égal à la somme des deux précédents:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,…
Il suffit de prendre deux nombres de départ. Les ajouter donne le troisième, puis le deuxième + le troisième donne le quatrième et ainsi de suite. Les termes de cette suite sont appelés nombres de Fibonacci.
La suite de Fibonacci possède de nombreuses propriétés très utilisées en mathématiques. Une d’entre elles est que le rapport de deux nombres consécutifs de la suite est alternativement supérieur et inférieur au nombre d’or, un nombre remarquable qui vaut exactement 1.61803398…
![]()
En effet: 13/8 = 1.625 ; 21/13 = 1.61538… ; 34/21 = 1.61904…et ainsi de suite…plus on avance dans la suite de Fibonacci, plus l’écart s’amenuise, et plus le rapport des deux nombres successifs (le plus grand / le plus petit) tend vers la valeur du nombre d’or 1,61803…!
En géométrie, le nombre d’or est la valeur qui correspond au rapport entre deux longueurs a (la plus grande) et b (la plus petite) telles que (a+b)/a = a/b.
Le nombre d’or était déjà utilisé par les Grecs, comme par exemple dans le Parthénon (le temple que les Grecs consacraient à certains de leurs dieux) dont le fronton est inscrit dans un rectangle dont les longueurs des côtés adjacents ont le nombre d’or comme rapport. Les peintres et architectes comme Botticelli, Dali ou Le Corbusier, pour ne citer qu’eux, l’ont utilisé dans leurs oeuvres. Le nombre d’or est souvent associé à des qualités esthétiques particulières et à des proportions harmonieuses. On constate aussi généralement que le rapport de la taille d’une personne avec la hauteur de son nombril est proche du nombre d’or…
Dans la nature, on retrouve très souvent des motifs basé sur la suite Fibonacci et sur le nombre d’or. Il semblerait que la nature marque une prédilection pour la suite de Fibonacci et pour le nombre d’or.
- les pommes de pins (pives)
- les marguerites
- les ananas
- les tournesols
- les cactus
- les étoiles de mer
- les coquilles de mollusques
- les galaxies
- les cyclones météorologiques
- …
On remarque par exemple que le nombre de pétales des fleurs est souvent un des nombres de la suite de Fibonacci: 3, 5, 8, 13, 21, 34 ou 55. Par exemple, les lis ont 3 pétales, les boutons d’or en ont 5, les chicorées en ont 21, les marguerites ont souvent 34 ou 55 pétales, etc…
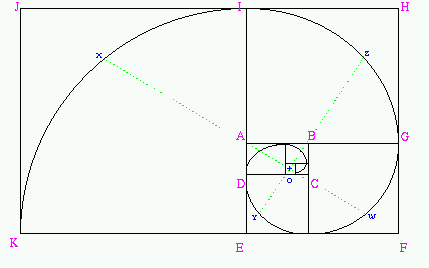
Dans certains objets de la nature, on observe aussi très souvent des spirales (spirales logarithmique) dans lesquelles intervient le nombre d’or. Cette spirale d’or s’inscrit dans un rectangle dont les proportions (rapport de la longueur sur la hauteur) correspondent au nombre d’or (on peut construire une spirale d’or en traçant des 1/4 de cercle dans chaque carré).
On observe de même sur de nombreux objets naturels que ces spirales forment des hélices et que le nombre d’hélices est intimement lié à la suite de Fibonacci. Si on observe l’arrangement des écailles qui s’alignent et s’enroulent autour d’une pomme de pin, on constate que chaque écaille appartient à deux hélices qui tournent en sens opposés, l’hélice “gauche” et l’hélice “droite”. Si on compte le nombre d’hélices droites et le nombre d’hélices gauches, on remarque que le couple de nombres que l’on obtient est formé de deux représentants successifs de la suite de Fibonacci:
Dans la photo ci-dessous, on compte 8 ou 5 spirales tournant respectivement vers la droite ou la gauche.
Les graines de tournesol forment aussi des hélices en spirale comme la pomme de pin.
Pour expliquer pourquoi la nature semble si proche des mathématiques, il faut prendre en compte la question d’efficacité dans ces arrangements géométriques, par exemple pour favoriser le processus de croissance des plantes et l’optimisation du remplissage de l’espace. On peut se poser la question si l”esthétique géométrique n’aurait-elle pas le même effet sur les abeilles que les couleurs des fleurs, aidant ainsi à la pollénisation et donc à la reproduction des plantes? Cette fonction esthétique de la suite de Fibonacci n’a en réalité pas clairement été démontrée…
En finance dans l’analyse technique des marchés financiers, on utilise un outil appelé retracement de Fibonacci. Les retracements de Fibonacci correspondent généralement à des supports ou à des résistances naturelles sur lesquels les prix vont buter. On se base donc sur l’idée que l’on peut prédire les mouvements boursiers en fonction de ratios ou seuils qui font référence à la suite de Fibonacci. Les ratios sont obtenus en divisant un nombre de la suite de Fibonacci par le nombre suivant. Sachant que tous les analystes financiers et les traders de la planète regardent ces ratios, ils ont de fait un caractère auto-réalisateur.
Dans le morceau Lateralus du groupe américain de rock progressif Tool, le rythme et le nombre de syllabes des paroles suivent la suite de Fibonacci.
Sources:
http://www.futura-sciences.com/fr/doc/t/mathematiques/d/larithmetique-et-les-plantes_63/c3/221/p3/